| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 3.1 | Example 1 & 2 (Before Exercise 3.2) | Exercise 3.2 |
| Example 3 to 6 (Before Exercise 3.3) | Exercise 3.3 | Example 7 & 8 (Before Exercise 3.4) |
| Exercise 3.4 | ||
Chapter 3 Understanding Quadrilaterals
Welcome to the solutions guide for Chapter 3: Understanding Quadrilaterals. This chapter significantly expands your geometric horizons beyond triangles, delving into the diverse world of polygons, with a particular emphasis on the properties and classifications of four-sided figures, or quadrilaterals. Polygons form the boundaries of countless objects in our world, and understanding their characteristics, especially those of quadrilaterals like rectangles, squares, and parallelograms, is fundamental to fields ranging from architecture and design to computer graphics and physics. This chapter builds a more formal understanding of these shapes and their defining attributes.
The exploration begins with the broader category of Polygons. Solutions clarify key concepts:
- Definition: A polygon is a simple closed curve made up entirely of straight line segments.
- Classification by Sides: Polygons are named based on their number of sides (e.g., triangle - 3 sides, quadrilateral - 4 sides, pentagon - 5 sides, hexagon - 6 sides, and so on).
- Convex vs. Concave: A polygon is convex if all its interior angles are less than $180^\circ$ (and all diagonals lie entirely within the polygon). It's concave if it has at least one interior angle greater than $180^\circ$ (and at least one diagonal lies partially or wholly outside).
- Regular vs. Irregular: A polygon is regular if it is both equiangular (all angles equal) and equilateral (all sides equal). Otherwise, it is irregular.
- Angle Sum Property: A crucial property for any convex polygon with $n$ sides is that the sum of its interior angles is given by the formula: $\text{Sum of interior angles} = (n-2) \times 180^\circ$. Solutions demonstrate applying this formula, for instance, to find the sum of angles in a pentagon ($n=5$) as $(5-2) \times 180^\circ = 3 \times 180^\circ = 540^\circ$, or to find a missing angle.
The primary focus then shifts to Quadrilaterals ($n=4$).
- Angle Sum Property: For any quadrilateral, applying the general formula gives $(4-2) \times 180^\circ = 2 \times 180^\circ = 360^\circ$. The solutions extensively use this property that the sum of the four interior angles is always $360^\circ$.
- Specific types are explored based on their unique properties:
- Trapezium: A quadrilateral with at least one pair of parallel sides.
- Kite: A quadrilateral with two distinct pairs of equal-length adjacent sides.
- Parallelogram: A quadrilateral with both pairs of opposite sides parallel. This is a key shape, and its properties are thoroughly covered in the solutions:
- Opposite sides are equal in length.
- Opposite angles are equal in measure.
- Consecutive angles are supplementary (their sum is $180^\circ$).
- The diagonals bisect each other (they cut each other exactly in half).
- Special Parallelograms:
- Rhombus: A parallelogram with all four sides equal. Its diagonals also bisect each other perpendicularly ($\perp$) and bisect the angles of the rhombus.
- Rectangle: A parallelogram with all four angles equal to $90^\circ$. Its diagonals are also equal in length.
- Square: A parallelogram that is both a rhombus and a rectangle. It possesses all properties of parallelograms, rhombuses, and rectangles (all sides equal, all angles $90^\circ$, diagonals equal, diagonals bisect each other perpendicularly).
Throughout the solutions, exercises involve identifying different quadrilaterals based on stated properties or markings on diagrams, and more frequently, calculating unknown side lengths or angle measures by applying the specific properties of the diagnosed shape. Each step in the reasoning process is clearly explained, often explicitly referencing the geometric property being used (e.g., "since opposite angles of a parallelogram are equal..." or "by the angle sum property of a quadrilateral..."). This approach is designed to strengthen not just knowledge of shapes, but also crucial deductive reasoning skills in geometry.
Exercise 3.1
Question 1. Given here are some figures.
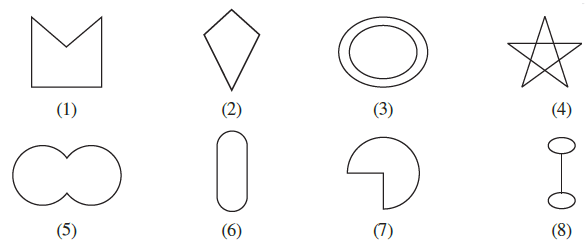
Classify each of them on the basis of the following.
(a) Simple curve
(b) Simple closed curve
(c) Polygon
(d) Convex polygon
(e) Concave polygon
Answer:
(a) Simple curve
A simple curve is a curve that can be drawn without lifting the pen from the paper and without crossing over itself.
Based on this definition, the following figures are simple curves: (1), (2), (5), (6), (7).
Reasoning:
- Figures (1), (2), (5), (6), and (7) can each be drawn in one continuous stroke without any part of the curve intersecting itself.
- Figure (3) is composed of two separate curves.
- Figure (4) crosses over itself.
- Figure (8) is composed of three separate parts.
(b) Simple closed curve
A simple closed curve is a simple curve whose starting and ending points are the same. It encloses an area.
The figures that are simple closed curves are: (1), (2), (5), (6), (7).
Reasoning:
- All the figures identified as simple curves in part (a) are also closed curves because their path begins and ends at the same point.
(c) Polygon
A polygon is a simple closed curve made up entirely of straight line segments.
The figures that are polygons are: (1), (2).
Reasoning:
- Figures (1) and (2) are simple closed curves and are formed exclusively by line segments.
- Figures (5), (6), and (7) are simple closed curves but contain curved parts, so they are not polygons.
- Figure (4) is made of line segments but is not a simple curve, so it is not a simple polygon.
(d) Convex polygon
A convex polygon is a polygon where all interior angles are less than 180°, and all its diagonals lie entirely inside the polygon.
The figure that is a convex polygon is: (2).
Reasoning:
- In figure (2), all interior angles are less than 180°. A line segment connecting any two points inside it would remain entirely within the figure.
(e) Concave polygon
A concave polygon is a polygon that has at least one interior angle greater than 180° (a reflex angle). At least one of its diagonals lies partially or wholly outside the polygon.
The figure that is a concave polygon is: (1).
Reasoning:
- Figure (1) has an interior angle at the top indentation that is greater than 180°. A diagonal connecting the top-left and top-right vertices would lie outside the shape.
Question 2. How many diagonals does each of the following have?
(a) A convex quadrilateral
(b) A regular hexagon
(c) A triangle
Answer:
The number of diagonals in a polygon with $n$ sides can be calculated using the formula: Number of diagonals = $\frac{n(n-3)}{2}$.
(a) A convex quadrilateral:
A quadrilateral has 4 sides.
Here, $n = 4$.
Number of diagonals = $\frac{4(4-3)}{2} = \frac{4(1)}{2} = \frac{4}{2} = 2$.
A convex quadrilateral has 2 diagonals.
(b) A regular hexagon:
A hexagon has 6 sides.
Here, $n = 6$.
Number of diagonals = $\frac{6(6-3)}{2} = \frac{6(3)}{2} = \frac{18}{2} = 9$.
A regular hexagon has 9 diagonals.
(c) A triangle:
A triangle has 3 sides.
Here, $n = 3$.
Number of diagonals = $\frac{3(3-3)}{2} = \frac{3(0)}{2} = \frac{0}{2} = 0$.
A triangle has 0 diagonals.
Question 3. What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)
Answer:
Sum of the measures of the angles of a convex quadrilateral
The sum of the measures of the angles of a convex quadrilateral is $360^\circ$.
We can show this in two ways:
Method 1: Using the angle sum formula for a polygon
The formula for the sum of the interior angles of a polygon with 'n' sides is given by:
Sum of angles = $(n-2) \times 180^\circ$
For a quadrilateral, the number of sides is $n = 4$.
Sum of angles = $(4-2) \times 180^\circ = 2 \times 180^\circ = 360^\circ$.
Method 2: Dividing the quadrilateral into triangles
Let's consider a convex quadrilateral ABCD. If we draw a diagonal, say AC, it divides the quadrilateral into two triangles: $\triangle ABC$ and $\triangle ADC$.
We know that the sum of angles in a triangle is $180^\circ$.
The sum of angles of the quadrilateral ABCD is the sum of the angles of $\triangle ABC$ and $\triangle ADC$.
Sum of angles of quadrilateral ABCD = (Sum of angles of $\triangle ABC$) + (Sum of angles of $\triangle ADC$)
$= 180^\circ + 180^\circ = 360^\circ$
Property for a non-convex quadrilateral
Yes, this property will hold even if the quadrilateral is not convex (i.e., it is a concave quadrilateral).
Let's consider a non-convex quadrilateral PQRS, which has a reflex angle at vertex R.
We can draw a diagonal, QS, that lies entirely inside the figure. This diagonal divides the non-convex quadrilateral into two triangles: $\triangle PQS$ and $\triangle RQS$.
The sum of the interior angles of the quadrilateral PQRS is the sum of the angles of these two triangles.
Sum of angles of quadrilateral PQRS = (Sum of angles of $\triangle PQS$) + (Sum of angles of $\triangle RQS$)
$= 180^\circ + 180^\circ = 360^\circ$
Thus, the sum of the measures of the angles of a quadrilateral is $360^\circ$, regardless of whether it is convex or non-convex.
Question 4. Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)
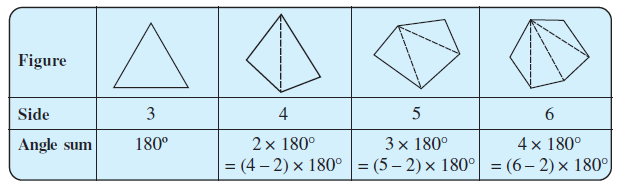
What can you say about the angle sum of a convex polygon with number of sides?
(a) 7
(b) 8
(c) 10
(d) n
Answer:
From the table, we observe that a convex polygon with $n$ sides can be divided into $(n-2)$ triangles.
The sum of the measures of the angles of a triangle is $180^\circ$.
Therefore, the sum of the measures of the angles of a convex polygon with $n$ sides is given by the formula:
Angle Sum = $(n-2) \times 180^\circ$
Now, let's find the angle sum for the given number of sides:
(a) 7 sides:
Here, $n = 7$.
Angle Sum = $(7-2) \times 180^\circ = 5 \times 180^\circ = 900^\circ$.
(b) 8 sides:
Here, $n = 8$.
Angle Sum = $(8-2) \times 180^\circ = 6 \times 180^\circ = 1080^\circ$.
(c) 10 sides:
Here, $n = 10$.
Angle Sum = $(10-2) \times 180^\circ = 8 \times 180^\circ = 1440^\circ$.
(d) n sides:
For a convex polygon with $n$ sides, the sum of the measures of its interior angles is $(n-2) \times 180^\circ$.
Question 5. What is a regular polygon?
State the name of a regular polygon of
(i) 3 sides
(ii) 4 sides
(iii) 6 sides
Answer:
A regular polygon is a polygon that is both equiangular (all angles have the same measure) and equilateral (all sides have the same length).
Now, let's state the names of regular polygons based on the number of sides:
(i) 3 sides: A regular polygon with 3 sides is called an equilateral triangle.
All sides are equal, and all angles are equal ($60^\circ$).
(ii) 4 sides: A regular polygon with 4 sides is called a square.
All sides are equal, and all angles are equal ($90^\circ$).
(iii) 6 sides: A regular polygon with 6 sides is called a regular hexagon.
All sides are equal, and all interior angles are equal ($120^\circ$).
Question 6. Find the angle measure x in the following figures.

Answer:
(a)
The given figure is a quadrilateral (a polygon with 4 sides).
We know that the sum of the measures of the interior angles of a quadrilateral is $360^\circ$.
The given angles are $50^\circ$, $130^\circ$, $120^\circ$, and $x$.
Therefore, we can set up the equation:
$50^\circ + 130^\circ + 120^\circ + x = 360^\circ$
Adding the known angles:
$300^\circ + x = 360^\circ$
Subtracting $300^\circ$ from both sides:
$x = 360^\circ - 300^\circ$
$x = 60^\circ$
(b)
The given figure is a quadrilateral (a polygon with 4 sides).
First, we need to find the fourth interior angle. The symbol on the outside indicates a right angle ($90^\circ$) with the straight line. The interior angle and this exterior right angle form a linear pair, so their sum is $180^\circ$. However, the symbol is on a straight line which implies the interior angle is also $90^\circ$ as it is perpendicular.
Let the interior angle be $y$.
$y + 90^\circ = 180^\circ$ (Linear pair)
$y = 180^\circ - 90^\circ = 90^\circ$
Now we have all four interior angles: $x$, $70^\circ$, $60^\circ$, and $90^\circ$.
The sum of the angles of a quadrilateral is $360^\circ$.
$x + 70^\circ + 60^\circ + 90^\circ = 360^\circ$
Adding the known angles:
$x + 220^\circ = 360^\circ$
Subtracting $220^\circ$ from both sides:
$x = 360^\circ - 220^\circ$
$x = 140^\circ$
(c)
The given figure is a pentagon (a polygon with 5 sides).
First, we need to find the two interior angles at the bottom. These angles form linear pairs with the given exterior angles.
Let the left interior angle be $a$.
$a + 70^\circ = 180^\circ$ (Linear pair)
$a = 180^\circ - 70^\circ = 110^\circ$
Let the right interior angle be $b$.
$b + 60^\circ = 180^\circ$ (Linear pair)
$b = 180^\circ - 60^\circ = 120^\circ$
Now, we find the sum of interior angles of a pentagon using the formula $(n-2) \times 180^\circ$, where $n=5$.
Sum of angles = $(5-2) \times 180^\circ = 3 \times 180^\circ = 540^\circ$.
The angles of the pentagon are $30^\circ$, $x$, $x$, $110^\circ$, and $120^\circ$.
$30^\circ + x + 110^\circ + 120^\circ + x = 540^\circ$
Combining like terms:
$2x + 260^\circ = 540^\circ$
$2x = 540^\circ - 260^\circ$
$2x = 280^\circ$
$x = \frac{280^\circ}{2}$
$x = 140^\circ$
(d)
The given figure is a pentagon (5 sides). The markings on the sides (double dashes) indicate that all sides are of equal length. This means it is a regular pentagon, and therefore all its interior angles are also equal.
All five interior angles are equal to $x$.
The sum of the interior angles of a pentagon is $(5-2) \times 180^\circ = 540^\circ$.
So, we can write the equation:
$x + x + x + x + x = 540^\circ$
$5x = 540^\circ$
$x = \frac{540^\circ}{5}$
$x = 108^\circ$
Question 7.
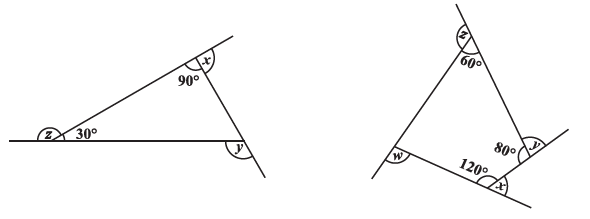
(a) Find x + y + z
(b) Find x + y + z + w
Answer:
(a) Find x + y + z
The figure is a triangle. The angles x, y, and z are the exterior angles of this triangle. Each exterior angle forms a linear pair with its adjacent interior angle.
First, let's find the values of x, y, and z individually.
Finding z:
$z + 30^\circ = 180^\circ$
(Linear pair)
$z = 180^\circ - 30^\circ = 150^\circ$
Finding x:
$x + 90^\circ = 180^\circ$
(Linear pair)
$x = 180^\circ - 90^\circ = 90^\circ$
Finding y:
To find y, we first need to find the third interior angle of the triangle. Let's call it 'a'.
By the angle sum property of a triangle, the sum of all interior angles is $180^\circ$.
$30^\circ + 90^\circ + a = 180^\circ$
$120^\circ + a = 180^\circ$
$a = 180^\circ - 120^\circ = 60^\circ$
Now, we can find y, as it forms a linear pair with angle 'a'.
$y + a = 180^\circ$
(Linear pair)
$y + 60^\circ = 180^\circ$
$y = 180^\circ - 60^\circ = 120^\circ$
Calculating the sum x + y + z:
$x + y + z = 90^\circ + 120^\circ + 150^\circ$
$x + y + z = 360^\circ$
(b) Find x + y + z + w
The figure is a quadrilateral. The angles x, y, z, and w are its exterior angles.
We know that the sum of the exterior angles of any convex polygon is $360^\circ$. Let's verify this by calculating each angle.
First, we need to find the fourth interior angle of the quadrilateral. Let's call it 'a'.
The sum of the interior angles of a quadrilateral is $360^\circ$.
$60^\circ + 80^\circ + 120^\circ + a = 360^\circ$
$260^\circ + a = 360^\circ$
$a = 360^\circ - 260^\circ = 100^\circ$
Now we can find the value of each exterior angle using the linear pair property:
Finding x:
$x + 120^\circ = 180^\circ$
(Linear pair)
$x = 180^\circ - 120^\circ = 60^\circ$
Finding y:
$y + 80^\circ = 180^\circ$
(Linear pair)
$y = 180^\circ - 80^\circ = 100^\circ$
Finding z:
$z + 60^\circ = 180^\circ$
(Linear pair)
$z = 180^\circ - 60^\circ = 120^\circ$
Finding w:
$w + a = 180^\circ$
(Linear pair)
$w + 100^\circ = 180^\circ$
$w = 180^\circ - 100^\circ = 80^\circ$
Calculating the sum x + y + z + w:
$x + y + z + w = 60^\circ + 100^\circ + 120^\circ + 80^\circ$
$x + y + z + w = 360^\circ$
Conclusion:
In both cases, the sum of the exterior angles is $360^\circ$. This illustrates a general property: The sum of the measures of the exterior angles of any convex polygon is $360^\circ$.
Example 1 & 2 (Before Exercise 3.2)
Example 1: Find measure x in Fig 3.9.
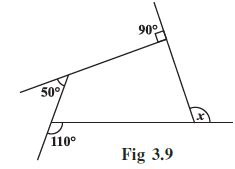
Answer:
Solution:
The figure shown is a polygon (specifically, a quadrilateral). The angles marked $x, 90^\circ, 50^\circ,$ and $110^\circ$ are all exterior angles of this polygon.
We will use the fundamental property of polygons:
The sum of the measures of the exterior angles of any convex polygon is $360^\circ$.
Based on this property, we can set up an equation by adding all the given exterior angles and equating their sum to $360^\circ$.
$x + 90^\circ + 50^\circ + 110^\circ = 360^\circ$
(Sum of exterior angles)
Now, we add the known angle measures:
$x + (90^\circ + 50^\circ + 110^\circ) = 360^\circ$
$x + 250^\circ = 360^\circ$
To find $x$, we subtract $250^\circ$ from both sides of the equation:
$x = 360^\circ - 250^\circ$
$x = 110^\circ$
Therefore, the measure of angle $x$ is $110^\circ$.
Alternate Solution (Using Interior Angles):
We can also solve this problem by first calculating the interior angles of the quadrilateral.
Each interior angle forms a linear pair with its corresponding exterior angle. The sum of angles in a linear pair is $180^\circ$.
Let's find the interior angles:
1. Interior angle adjacent to $90^\circ = 180^\circ - 90^\circ = 90^\circ$.
2. Interior angle adjacent to $50^\circ = 180^\circ - 50^\circ = 130^\circ$.
3. Interior angle adjacent to $110^\circ = 180^\circ - 110^\circ = 70^\circ$.
Let the fourth interior angle (adjacent to $x$) be 'a'.
The sum of the interior angles of a quadrilateral is $(4-2) \times 180^\circ = 360^\circ$.
$90^\circ + 130^\circ + 70^\circ + a = 360^\circ$
$290^\circ + a = 360^\circ$
$a = 360^\circ - 290^\circ$
$a = 70^\circ$
Now, the angle $x$ and the interior angle 'a' form a linear pair.
$x + a = 180^\circ$
(Linear pair)
$x + 70^\circ = 180^\circ$
$x = 180^\circ - 70^\circ$
$x = 110^\circ$
Both methods give the same result. The measure of angle $x$ is $110^\circ$.
Example 2: Find the number of sides of a regular polygon whose each exterior angle has a measure of 45°.
Answer:
Given: The measure of each exterior angle of a regular polygon is $45^\circ$.
To Find: The number of sides of the regular polygon.
Solution:
We know that the sum of the measures of the exterior angles of any convex polygon is always $360^\circ$.
For a regular polygon, all exterior angles are equal in measure.
Let the number of sides of the regular polygon be $n$.
The measure of each exterior angle of a regular polygon with $n$ sides is given by the formula: $\frac{360^\circ}{n}$.
We are given that the measure of each exterior angle is $45^\circ$.
So, we can set up the equation:
$\frac{360^\circ}{n} = 45^\circ$
... (i)
To find $n$, we can rearrange the equation:
$n = \frac{360^\circ}{45^\circ}$
$n = 8$
The number of sides of the regular polygon is 8.
Exercise 3.2
Question 1. Find x in the following figures.

Answer:
We know that the sum of the measures of the exterior angles of any convex polygon is $360^\circ$.
(a)
The given figure is a triangle.
The exterior angles are $125^\circ$, $125^\circ$, and $x$.
The sum of the exterior angles is $360^\circ$.
Therefore,
$125^\circ + 125^\circ + x = 360^\circ$
... (i)
$250^\circ + x = 360^\circ$
$x = 360^\circ - 250^\circ$
$x = 110^\circ$
The value of $x$ is $110^\circ$.
(b)
The given figure is a pentagon (5 sides).
The exterior angles are $90^\circ$, $60^\circ$, $90^\circ$, $70^\circ$, and $x$. Note that the square symbol indicates an exterior angle of $90^\circ$.
The sum of the exterior angles is $360^\circ$.
Therefore,
$90^\circ + 60^\circ + 90^\circ + 70^\circ + x = 360^\circ$
... (i)
$310^\circ + x = 360^\circ$
$x = 360^\circ - 310^\circ$
$x = 50^\circ$
The value of $x$ is $50^\circ$.
Question 2. Find the measure of each exterior angle of a regular polygon of
(i) 9 sides
(ii) 15 sides
Answer:
We know that the sum of the measures of the exterior angles of any convex polygon is $360^\circ$.
For a regular polygon with $n$ sides, all exterior angles are equal in measure.
The measure of each exterior angle of a regular polygon with $n$ sides is given by the formula: $\frac{360^\circ}{n}$.
(i) 9 sides:
Here, the number of sides $n = 9$.
Measure of each exterior angle = $\frac{360^\circ}{9}$
Measure of each exterior angle = $40^\circ$.
The measure of each exterior angle of a regular polygon with 9 sides is $40^\circ$.
(ii) 15 sides:
Here, the number of sides $n = 15$.
Measure of each exterior angle = $\frac{360^\circ}{15}$
Measure of each exterior angle = $24^\circ$.
The measure of each exterior angle of a regular polygon with 15 sides is $24^\circ$.
Question 3. How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Answer:
Given: The measure of an exterior angle of a regular polygon is $24^\circ$.
To Find: The number of sides of the regular polygon.
Solution:
We know that the sum of the measures of the exterior angles of any convex polygon is always $360^\circ$.
For a regular polygon, all exterior angles have the same measure.
Let the number of sides of the regular polygon be $n$.
The measure of each exterior angle of a regular polygon with $n$ sides is given by the formula: $\frac{360^\circ}{n}$.
We are given that the measure of an exterior angle is $24^\circ$.
So, we have:
$\frac{360^\circ}{n} = 24^\circ$
... (i)
To find $n$, we can rearrange the equation:
$n = \frac{360^\circ}{24^\circ}$
Now, we perform the division:
$n = 15$
The regular polygon has 15 sides.
Question 4. How many sides does a regular polygon have if each of its interior angles is 165°?
Answer:
Given: The measure of each interior angle of a regular polygon is $165^\circ$.
To Find: The number of sides of the regular polygon.
Solution:
For any polygon, the sum of the interior angle and its corresponding exterior angle at any vertex is $180^\circ$ (they form a linear pair).
Measure of each exterior angle = $180^\circ - \text{Measure of each interior angle}$
Measure of each exterior angle = $180^\circ - 165^\circ$
Measure of each exterior angle = $15^\circ$.
We know that the sum of the measures of the exterior angles of any convex polygon is $360^\circ$.
For a regular polygon with $n$ sides, all exterior angles have the same measure.
The measure of each exterior angle of a regular polygon with $n$ sides is also given by the formula: $\frac{360^\circ}{n}$.
So, we can set up the equation:
$\frac{360^\circ}{n} = 15^\circ$
... (i)
To find $n$, we rearrange the equation:
$n = \frac{360^\circ}{15^\circ}$
Performing the division:
$n = 24$
The regular polygon has 24 sides.
Question 5.
(a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?
(b) Can it be an interior angle of a regular polygon? Why?
Answer:
(a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?
We know that the sum of the measures of the exterior angles of any convex polygon is $360^\circ$.
For a regular polygon with $n$ sides, all exterior angles are equal in measure. The measure of each exterior angle is given by the formula: $\frac{360^\circ}{n}$.
If the measure of each exterior angle is $22^\circ$, then:
$\frac{360^\circ}{n} = 22^\circ$
... (i)
To find the number of sides $n$, we rearrange the equation:
$n = \frac{360}{22}$
Simplifying the fraction:
$n = \frac{\cancel{360}^{180}}{\cancel{22}_{11}}$
$n = \frac{180}{11}$
Since $\frac{180}{11}$ is not an integer, a polygon cannot have $\frac{180}{11}$ sides.
The number of sides of a polygon must be a whole number.
Therefore, it is not possible to have a regular polygon with a measure of each exterior angle as $22^\circ$.
(b) Can it be an interior angle of a regular polygon? Why?
If $22^\circ$ is an interior angle of a regular polygon, we can find the measure of the corresponding exterior angle.
The sum of an interior angle and its corresponding exterior angle at any vertex is $180^\circ$.
Measure of each exterior angle = $180^\circ - \text{Measure of each interior angle}$
Exterior angle = $180^\circ - 22^\circ = 158^\circ$
... (i)
Now, we check if $158^\circ$ can be the measure of an exterior angle of a regular polygon.
Using the formula for the measure of each exterior angle of a regular polygon with $n$ sides: $\frac{360^\circ}{n}$.
If the measure of each exterior angle is $158^\circ$, then:
$\frac{360^\circ}{n} = 158^\circ$
... (ii)
To find the number of sides $n$, we rearrange the equation:
$n = \frac{360}{158}$
Simplifying the fraction:
$n = \frac{\cancel{360}^{180}}{\cancel{158}_{79}}$
$n = \frac{180}{79}$
Since $\frac{180}{79}$ is not an integer, a polygon cannot have $\frac{180}{79}$ sides.
The number of sides of a polygon must be a whole number.
Therefore, $22^\circ$ cannot be an interior angle of a regular polygon.
Reason (Why?): For a regular polygon, the number of sides must be a positive integer. If $22^\circ$ were either an interior or an exterior angle, the calculation for the number of sides $n$ results in a non-integer value ($\frac{180}{11}$ for exterior and $\frac{180}{79}$ for interior), which is not possible for a polygon.
Question 6.
(a) What is the minimum interior angle possible for a regular polygon? Why?
(b) What is the maximum exterior angle possible for a regular polygon?
Answer:
(a) What is the minimum interior angle possible for a regular polygon? Why?
The minimum interior angle possible for a regular polygon is $60^\circ$.
Reason:
A polygon is a closed figure with at least 3 straight sides. A regular polygon has all sides and all interior angles equal. Therefore, the regular polygon with the minimum number of sides is an equilateral triangle, which has 3 sides.
The formula for the measure of each interior angle of a regular polygon with 'n' sides is:
Interior Angle = $\frac{(n-2) \times 180^\circ}{n}$
For an equilateral triangle, $n=3$. Substituting this into the formula:
Interior Angle = $\frac{(3-2) \times 180^\circ}{3} = \frac{1 \times 180^\circ}{3} = 60^\circ$
As the number of sides (n) of a regular polygon increases, the measure of its interior angle also increases. For example:
- Square (n=4): Interior angle = $\frac{(4-2) \times 180^\circ}{4} = 90^\circ$
- Regular Pentagon (n=5): Interior angle = $\frac{(5-2) \times 180^\circ}{5} = 108^\circ$
Since the interior angle increases with the number of sides, the minimum possible interior angle must belong to the regular polygon with the minimum number of sides, which is the equilateral triangle. Hence, the minimum interior angle is $60^\circ$.
(b) What is the maximum exterior angle possible for a regular polygon?
The maximum exterior angle possible for a regular polygon is $120^\circ$.
Reason:
There are two ways to determine this:
Method 1: Using the relationship between interior and exterior angles.
For any polygon, the interior angle and its corresponding exterior angle are supplementary (add up to $180^\circ$).
Exterior Angle = $180^\circ$ - Interior Angle
To get the maximum possible exterior angle, we must use the minimum possible interior angle. From part (a), we know the minimum interior angle for a regular polygon is $60^\circ$.
Maximum Exterior Angle = $180^\circ - 60^\circ = 120^\circ$.
Method 2: Using the exterior angle formula.
The sum of all exterior angles of any convex polygon is always $360^\circ$. For a regular polygon with 'n' sides, all exterior angles are equal. Therefore, the measure of each exterior angle is:
Exterior Angle = $\frac{360^\circ}{n}$
To maximize the value of this fraction, we must minimize the denominator 'n' (the number of sides). The minimum number of sides a polygon can have is 3.
Substituting $n=3$ into the formula:
Maximum Exterior Angle = $\frac{360^\circ}{3} = 120^\circ$.
Example 3 to 6 (Before Exercise 3.3)
Example 3: Find the perimeter of the parallelogram PQRS (Fig 3.2).
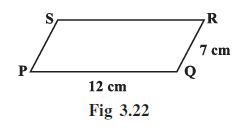
Answer:
Given: A parallelogram PQRS with side lengths PQ = 12 cm and QR = 7 cm.
To Find: The perimeter of the parallelogram PQRS.
Solution:
We know that opposite sides of a parallelogram are equal in length.
In parallelogram PQRS:
PQ = RS
(Opposite sides of a parallelogram)
QR = SP
(Opposite sides of a parallelogram)
Given PQ = 12 cm and QR = 7 cm.
So, RS = 12 cm and SP = 7 cm.
The perimeter of a polygon is the sum of the lengths of its sides.
Perimeter of parallelogram PQRS = PQ + QR + RS + SP
Perimeter = 12 cm + 7 cm + 12 cm + 7 cm
... (i)
Perimeter = (12 + 12) cm + (7 + 7) cm
Perimeter = 24 cm + 14 cm
Perimeter = 38 cm
The perimeter of the parallelogram PQRS is 38 cm.
Example 4: In Fig 3.26, BEST is a parallelogram. Find the values x, y and z.
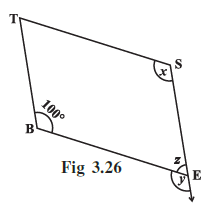
Answer:
Given: BEST is a parallelogram with $\angle B = 100^\circ$.
We need to find the values of x, y, and z using the properties of a parallelogram.
Step 1: Finding the value of x
In a parallelogram, opposite angles are equal in measure.
In parallelogram BEST, the angle at vertex S (which is $x$) is opposite to the angle at vertex B (which is $100^\circ$).
$x = \angle B$
(Opposite angles of a parallelogram)
Therefore, $x = 100^\circ$.
Step 2: Finding the value of z
In a parallelogram, consecutive (or adjacent) angles are supplementary, which means their sum is $180^\circ$.
The angle at vertex B and the angle at vertex E (which is $z$) are consecutive angles.
$\angle B + z = 180^\circ$
(Consecutive angles of a parallelogram)
Substituting the value of $\angle B$:
$100^\circ + z = 180^\circ$
$z = 180^\circ - 100^\circ$
Therefore, $z = 80^\circ$.
Step 3: Finding the value of y
The interior angle $z$ and the exterior angle $y$ at vertex E form a linear pair because they are adjacent angles on a straight line.
The sum of angles in a linear pair is $180^\circ$.
$y + z = 180^\circ$
(Linear pair)
Substituting the value of $z$ that we found:
$y + 80^\circ = 180^\circ$
$y = 180^\circ - 80^\circ$
Therefore, $y = 100^\circ$.
The final values are:
$x = 100^\circ$
$y = 100^\circ$
$z = 80^\circ$
Example 5: In a parallelogram RING, (Fig 3.28) if m∠R = 70°, find all the other angles.
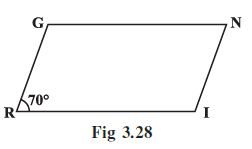
Answer:
Given: RING is a parallelogram and m$\angle$R = $70^\circ$.
To Find: The measures of the other angles: m$\angle$I, m$\angle$N, and m$\angle$G.
Solution:
In a parallelogram, opposite angles are equal.
Therefore, $\angle$R and $\angle$N are opposite angles, so m$\angle$N = m$\angle$R.
m$\angle$N = $70^\circ$
... (i)
Also, in a parallelogram, adjacent angles are supplementary (their sum is $180^\circ$).
Angles $\angle$R and $\angle$I are adjacent angles.
m$\angle$R + m$\angle$I = $180^\circ$
(Adjacent angles are supplementary)
70$^\circ$ + m$\angle$I = $180^\circ$
... (ii)
m$\angle$I = $180^\circ - 70^\circ$
m$\angle$I = $110^\circ$
Now, we can find m$\angle$G. Angles $\angle$G and $\angle$I are opposite angles, so m$\angle$G = m$\angle$I.
m$\angle$G = $110^\circ$
... (iii)
Alternatively, angles $\angle$R and $\angle$G are adjacent angles.
m$\angle$R + m$\angle$G = $180^\circ$
(Adjacent angles are supplementary)
70$^\circ$ + m$\angle$G = $180^\circ$
... (iv)
m$\angle$G = $180^\circ - 70^\circ$
m$\angle$G = $110^\circ$
The other angles of the parallelogram RING are m$\angle$I = $110^\circ$, m$\angle$N = $70^\circ$, and m$\angle$G = $110^\circ$.
Example 6: In Fig 3.31 HELP is a parallelogram. (Lengths are in cms). Given that OE = 4 and HL is 5 more than PE? Find OH.
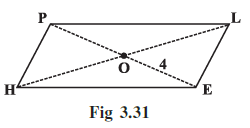
Answer:
Given: HELP is a parallelogram. O is the intersection point of the diagonals. OE = 4 cm. HL is 5 cm more than PE.
To Find: The length of OH.
Solution:
In a parallelogram, the diagonals bisect each other.
The diagonals of parallelogram HELP are HL and PE. They bisect each other at point O.
Since the diagonals bisect each other, O is the midpoint of both PE and HL.
We are given that OE = 4 cm.
OE = OP = 4 cm
(Diagonals bisect each other)
The length of diagonal PE is the sum of OE and OP.
PE = OE + OP
... (i)
PE = 4 cm + 4 cm = 8 cm.
We are given that HL is 5 cm more than PE.
HL = PE + 5 cm
(Given)
HL = 8 cm + 5 cm = 13 cm
... (ii)
Since O is the midpoint of diagonal HL, the length of OH is half the length of HL.
OH = $\frac{1}{2}$ HL
(Diagonals bisect each other)
OH = $\frac{1}{2} \times 13$ cm
... (iii)
OH = $\frac{13}{2}$ cm = 6.5 cm.
The length of OH is 6.5 cm.
Exercise 3.3
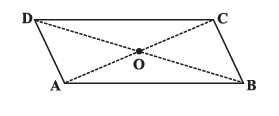
Question 1. Given a parallelogram ABCD. Complete each statement along with the definition or property used.
(i) AD = ......
(ii) ∠DCB = ......
(iii) OC =
(iv) m∠DAB + m∠CDA = ...…
Answer:
(i) AD = BC
Property: In a parallelogram, opposite sides are equal in length.
(ii) $\angle$DCB = $\angle$DAB
Property: In a parallelogram, opposite angles are equal.
(iii) OC = OA
Property: In a parallelogram, diagonals bisect each other.
(iv) m$\angle$DAB + m$\angle$CDA = 180°
Property: In a parallelogram, adjacent angles are supplementary (their sum is 180°).
Question 2. Consider the following parallelograms. Find the values of the unknowns x, y, z.

Answer:
(i)
The given figure ABCD is a parallelogram.
Finding y:
In a parallelogram, opposite angles are equal.
$y = \angle B = 100^\circ$
(Opposite angles of a parallelogram)
Finding x and z:
In a parallelogram, consecutive (adjacent) angles are supplementary (their sum is $180^\circ$).
$x + 100^\circ = 180^\circ$
(Consecutive angles are supplementary)
$x = 180^\circ - 100^\circ = 80^\circ$
Since opposite angles are equal, $z$ is opposite to $x$.
$z = x = 80^\circ$
(Opposite angles of a parallelogram)
Thus, $x = 80^\circ, y = 100^\circ, z = 80^\circ$.
(ii)
The given figure is a parallelogram.
Finding x and y:
Consecutive angles in a parallelogram are supplementary.
$x + 50^\circ = 180^\circ$
(Consecutive angles are supplementary)
$x = 180^\circ - 50^\circ = 130^\circ$
Opposite angles in a parallelogram are equal.
$y = x = 130^\circ$
(Opposite angles of a parallelogram)
Finding z:
The interior angle opposite the given $50^\circ$ angle is also $50^\circ$. This interior angle and the exterior angle $z$ form a linear pair.
$z + 50^\circ = 180^\circ$
(Linear pair)
$z = 180^\circ - 50^\circ = 130^\circ$
Thus, $x = 130^\circ, y = 130^\circ, z = 130^\circ$.
(iii)
The figure is a rhombus (a type of parallelogram) since its diagonals intersect at a right angle.
Finding x:
The angle $x$ and the $90^\circ$ angle are vertically opposite angles.
$x = 90^\circ$
(Vertically opposite angles)
Finding y:
Consider the triangle formed by the intersection. The sum of its angles is $180^\circ$.
$y + x + 30^\circ = 180^\circ$
$y + 90^\circ + 30^\circ = 180^\circ$
$y + 120^\circ = 180^\circ$
$y = 180^\circ - 120^\circ = 60^\circ$
Finding z:
Since the opposite sides of a rhombus are parallel, the diagonal acts as a transversal. The angles $y$ and $z$ are alternate interior angles.
$z = y = 60^\circ$
(Alternate interior angles)
Thus, $x = 90^\circ, y = 60^\circ, z = 60^\circ$.
(iv)
The given figure is a parallelogram.
Finding y:
Opposite angles of a parallelogram are equal.
$y = 80^\circ$
(Opposite angles of a parallelogram)
Finding x:
Consecutive angles are supplementary.
$x + 80^\circ = 180^\circ$
(Consecutive angles are supplementary)
$x = 180^\circ - 80^\circ = 100^\circ$
Finding z:
The angle $z$ and the interior angle $80^\circ$ are corresponding angles, as the top and bottom sides are parallel.
$z = 80^\circ$
(Corresponding angles)
Thus, $x = 100^\circ, y = 80^\circ, z = 80^\circ$.
(v)
The given figure is a parallelogram.
Finding y:
Opposite angles of a parallelogram are equal.
$y = 112^\circ$
(Opposite angles of a parallelogram)
Finding z:
The angles $y$ and $(40^\circ+z)$ are consecutive angles, so their sum is $180^\circ$.
$y + (40^\circ + z) = 180^\circ$
(Consecutive angles are supplementary)
$112^\circ + 40^\circ + z = 180^\circ$
$152^\circ + z = 180^\circ$
$z = 180^\circ - 152^\circ = 28^\circ$
Finding x:
The top and bottom sides are parallel, and the diagonal is a transversal. Therefore, angles $x$ and $z$ are alternate interior angles.
$x = z = 28^\circ$
(Alternate interior angles)
Thus, $x = 28^\circ, y = 112^\circ, z = 28^\circ$.
Question 3. Can a quadrilateral ABCD be a parallelogram if
(i) ∠D + ∠B = 180°?
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
(iii) ∠A = 70° and ∠C = 65°?
Answer:
(i) Can a quadrilateral ABCD be a parallelogram if ∠D + ∠B = 180°?
A quadrilateral can be a parallelogram if this condition is met, but it is not a necessary condition for all cases. The primary property for angles in a parallelogram is that opposite angles must be equal.
Let's consider the properties:
1. Condition for a parallelogram: The opposite angles must be equal, i.e., $\angle D = \angle B$.
2. Given condition: $\angle D + \angle B = 180^\circ$.
If we apply both conditions simultaneously, we get:
$\angle B + \angle B = 180^\circ \implies 2\angle B = 180^\circ \implies \angle B = 90^\circ$.
This means $\angle D$ would also be $90^\circ$. This is true for shapes like a rectangle or a square, which are types of parallelograms.
However, a quadrilateral that is not a parallelogram can also satisfy this condition. For example, an isosceles trapezium is a cyclic quadrilateral, and the sum of its opposite angles is $180^\circ$, but it is not a parallelogram.
Therefore, the quadrilateral ABCD can be, but does not have to be, a parallelogram. The condition is not sufficient on its own.
(ii) Can a quadrilateral ABCD be a parallelogram if AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
No, this quadrilateral cannot be a parallelogram.
Reason:
A fundamental property of a parallelogram is that its opposite sides must be equal in length. This means two conditions must be met:
1. AB = DC
2. AD = BC
In the given measurements:
AB = DC = 8 cm (This condition is met)
But, AD = 4 cm and BC = 4.4 cm, which means AD ≠ BC.
Since one pair of opposite sides is not equal, the quadrilateral ABCD cannot be a parallelogram.
(iii) Can a quadrilateral ABCD be a parallelogram if ∠A = 70° and ∠C = 65°?
No, this quadrilateral cannot be a parallelogram.
Reason:
A fundamental property of a parallelogram is that its opposite angles must be equal in measure. In quadrilateral ABCD, ∠A and ∠C are opposite angles.
According to the given values:
$\angle A = 70^\circ$ and $\angle C = 65^\circ$.
Since $\angle A \neq \angle C$, the condition that opposite angles must be equal is violated.
Therefore, the quadrilateral ABCD cannot be a parallelogram.
Question 4. Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
Answer:
A quadrilateral that is not a parallelogram but has exactly one pair of equal opposite angles is a kite.
Description:
A kite is a quadrilateral that has two pairs of equal-length sides that are adjacent to each other. It is not a parallelogram because its opposite sides are not equal or parallel.
Let's consider a kite ABCD:
- It has adjacent sides equal: AB = AD and CB = CD.
- It is not a parallelogram because AB ≠ CD and AD ≠ CB.
- It has exactly one pair of opposite angles that are equal. The angles between the pairs of unequal sides are equal. In this case, $\angle B = \angle D$.
- The other pair of opposite angles are not equal, i.e., $\angle A \neq \angle C$.
Therefore, a kite fits the description perfectly.
Rough Figure:
Below is a rough figure of a kite ABCD where $\angle B = \angle D$.
Question 5. The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
Answer:
Given:
The ratio of the measures of two adjacent angles of a parallelogram is $3:2$.
To Find:
The measure of each of the angles of the parallelogram.
Solution:
Let the measures of the two adjacent angles of the parallelogram be $3x$ and $2x$, according to the given ratio.
We know that the sum of adjacent angles in a parallelogram is $180^\circ$ (they are supplementary).
$3x + 2x = 180^\circ$
(Adjacent angles are supplementary)
Combine the terms on the left side:
$5x = 180^\circ$
Divide both sides by 5 to find the value of $x$:
$x = \frac{180^\circ}{5}$
$x = 36^\circ$
Now, we can find the measure of the two adjacent angles:
First angle $= 3x = 3 \times 36^\circ$
First angle $= 108^\circ$
Second angle $= 2x = 2 \times 36^\circ$
Second angle $= 72^\circ$
In a parallelogram, opposite angles are equal.
So, the angles of the parallelogram are $108^\circ$, $72^\circ$, $108^\circ$, and $72^\circ$.
We can verify this: $108^\circ + 72^\circ + 108^\circ + 72^\circ = 360^\circ$ (Sum of angles in a quadrilateral is $360^\circ$), and adjacent angles sum to $108^\circ + 72^\circ = 180^\circ$.
The measures of the angles of the parallelogram are $108^\circ$, $72^\circ$, $108^\circ$, and $72^\circ$.
Question 6. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
Answer:
Given:
Two adjacent angles of a parallelogram have equal measure.
To Find:
The measure of each of the angles of the parallelogram.
Solution:
Let the measure of the two adjacent angles of the parallelogram be $a$. Since they have equal measure, both adjacent angles are equal to $a$.
We know that the sum of adjacent angles in a parallelogram is $180^\circ$ (they are supplementary).
$a + a = 180^\circ$
(Adjacent angles are supplementary)
Combine the terms on the left side:
$2a = 180^\circ$
Divide both sides by 2 to find the value of $a$:
$a = \frac{180^\circ}{2}$
$a = 90^\circ$
So, the two adjacent angles are each $90^\circ$.
In a parallelogram, opposite angles are equal.
Since one pair of adjacent angles are $90^\circ$, the opposite angle to the first $90^\circ$ angle is also $90^\circ$. The opposite angle to the second $90^\circ$ angle is also $90^\circ$.
Therefore, all four angles of the parallelogram are $90^\circ$.
A parallelogram with all angles equal to $90^\circ$ is a rectangle.
The measure of each angle of the parallelogram is $90^\circ$.
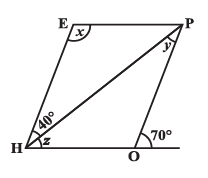
Question 7. The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
Answer:
Solution:
The given figure HOPE is a parallelogram. We need to find the values of x, y, and z by using the properties of parallelograms and lines.
Step 1: Finding the interior angle at vertex O
Let the interior angle at vertex O be $\angle POH$. This angle and the given exterior angle of $70^\circ$ form a linear pair, so their sum is $180^\circ$.
$\angle POH + 70^\circ = 180^\circ$
(Linear Pair)
$\angle POH = 180^\circ - 70^\circ$
$\angle POH = 110^\circ$
Step 2: Finding the value of x
In a parallelogram, opposite angles are equal. The angle $x$ (which is $\angle PEH$) is opposite to the interior angle at O ($\angle POH$).
$x = \angle POH$
(Opposite angles of a parallelogram are equal)
Therefore, $x = 110^\circ$.
Step 3: Finding the value of y
In a parallelogram, opposite sides are parallel. Therefore, EP is parallel to HO (EP || HO). The line segment HP acts as a transversal.
The angle $y$ and the angle $40^\circ$ are alternate interior angles. Alternate interior angles are equal.
$y = 40^\circ$
(Alternate interior angles)
Therefore, $y = 40^\circ$.
Step 4: Finding the value of z
In a parallelogram, adjacent (or consecutive) angles are supplementary, meaning their sum is $180^\circ$. The angle at vertex H ($\angle EHO$) and the angle at vertex E ($\angle PEH$) are adjacent angles.
The full angle at H is $\angle EHO = 40^\circ + z$.
The angle at E is $\angle PEH = x = 110^\circ$.
$\angle EHO + \angle PEH = 180^\circ$
(Consecutive angles are supplementary)
Substituting the values:
$(40^\circ + z) + 110^\circ = 180^\circ$
$z + 150^\circ = 180^\circ$
$z = 180^\circ - 150^\circ$
Therefore, $z = 30^\circ$.
The final values for the angles are:
$x = 110^\circ$
$y = 40^\circ$
$z = 30^\circ$
Question 8. The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)

Answer:
(i) Parallelogram GUNS
In a parallelogram, the lengths of opposite sides are equal.
Finding y:
The side GU is opposite to the side SN.
GU = SN
(Opposite sides of a parallelogram are equal)
$3y - 1 = 26$
$3y = 26 + 1$
$3y = 27$
$y = \frac{27}{3}$
$y = 9$
Finding x:
The side GS is opposite to the side NU.
GS = NU
(Opposite sides of a parallelogram are equal)
$3x = 18$
$x = \frac{18}{3}$
$x = 6$
Therefore, for the parallelogram GUNS, $x = 6$ and $y = 9$.
(ii) Parallelogram RUNS
In a parallelogram, the diagonals bisect each other. This means they cut each other into two equal segments at their point of intersection.
Finding y:
The diagonal SU is bisected. Therefore, the two segments are equal.
$y + 7 = 20$
(Diagonals of a parallelogram bisect each other)
$y = 20 - 7$
$y = 13$
Finding x:
The diagonal RN is also bisected. Therefore, its two segments are equal.
$x + y = 16$
(Diagonals of a parallelogram bisect each other)
Now, we substitute the value of y we found into this equation:
$x + 13 = 16$
$x = 16 - 13$
$x = 3$
Therefore, for the parallelogram RUNS, $x = 3$ and $y = 13$.
Question 9.

In the above figure both RISK and CLUE are parallelograms. Find the value of x.
Answer:
Given:
The figure contains two parallelograms: RISK and CLUE.
To Find:
The value of x.
Solution:
To find the value of x, we need to find the other two angles of the small triangle formed by the intersection of the two parallelograms. Let's call the intersection point O. The triangle is $\triangle EOS$. We will find the angles $\angle OES$ and $\angle OSE$ using the properties of the parallelograms.
Step 1: Find $\angle OSE$ using parallelogram RISK.
In any parallelogram, the adjacent angles are supplementary, meaning their sum is $180^\circ$. In parallelogram RISK, the angle at vertex K ($\angle RKS$) and the angle at vertex S ($\angle ISK$) are adjacent.
$\angle K + \angle S = 180^\circ$
(Adjacent angles of a parallelogram)
We are given $\angle K = 120^\circ$.
$120^\circ + \angle S = 180^\circ$
$\angle S = 180^\circ - 120^\circ$
$\angle S = 60^\circ$
This angle is one of the angles in our triangle, so $\angle OSE = 60^\circ$.
Step 2: Find $\angle OES$ using parallelogram CLUE.
In any parallelogram, the opposite angles are equal. In parallelogram CLUE, the angle at vertex E ($\angle CEU$) is opposite to the angle at vertex L ($\angle CLU$).
$\angle E = \angle L$
(Opposite angles of a parallelogram)
We are given $\angle L = 70^\circ$.
Therefore, $\angle E = 70^\circ$.
This angle is the second angle in our triangle, so $\angle OES = 70^\circ$.
Step 3: Find x using the Angle Sum Property of a Triangle.
Now, we consider the triangle $\triangle EOS$. The sum of the measures of the angles in any triangle is $180^\circ$.
$x + \angle OES + \angle OSE = 180^\circ$
(Angle sum property of a triangle)
Substituting the values we found in the previous steps:
$x + 70^\circ + 60^\circ = 180^\circ$
$x + 130^\circ = 180^\circ$
Subtracting $130^\circ$ from both sides:
$x = 180^\circ - 130^\circ$
$x = 50^\circ$
Therefore, the value of $x$ is $50^\circ$.
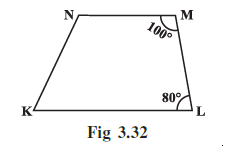
Question 10. Explain how this figure is a trapezium. Which of its two sides are parallel? (Fig 3.32)
Answer:
Explanation of how the figure is a trapezium:
A trapezium (or trapezoid) is a quadrilateral with at least one pair of parallel sides.
To determine if the figure KLMN is a trapezium, we need to check if any pair of opposite sides are parallel. We can do this by using the property of a transversal line intersecting two other lines.
Let's consider the sides NM and KL as two lines and the side ML as a transversal intersecting them.
The angles $\angle M$ and $\angle L$ are the interior angles on the same side of the transversal ML. According to the properties of parallel lines, if the sum of these interior angles is $180^\circ$, then the lines NM and KL are parallel.
Let's calculate the sum of the given angles:
Sum of adjacent angles = $\angle M + \angle L$
$ = 100^\circ + 80^\circ$
$ = 180^\circ$
Since the sum of the consecutive interior angles is $180^\circ$, the lines NM and KL are parallel to each other.
Because the quadrilateral KLMN has one pair of parallel opposite sides (NM || KL), it is a trapezium.
Which of its two sides are parallel?
Based on the explanation above, the two parallel sides are NM and KL.
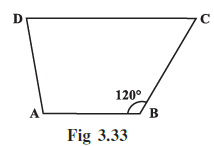
Question 11. Find m∠C in Fig 3.33 if $\overline{AB}$ || $\overline{DC}$ .
Answer:
Given:
The figure is a trapezium ABCD, where the side $\overline{AB}$ is parallel to the side $\overline{DC}$ (AB || DC).
The measure of angle B is given as $m\angle B = 120^\circ$.
To Find:
The measure of angle C ($m\angle C$).
Solution:
We can find the measure of angle C using the property of parallel lines intersected by a transversal.
Since it is given that AB || DC, we can consider the line segment BC as a transversal intersecting these two parallel lines.
When a transversal intersects two parallel lines, the sum of the consecutive interior angles (or the interior angles on the same side of the transversal) is $180^\circ$.
In this case, $\angle B$ and $\angle C$ are consecutive interior angles.
$m\angle B + m\angle C = 180^\circ$
(Sum of consecutive interior angles is $180^\circ$)
We are given that $m\angle B = 120^\circ$. Substituting this value into the equation:
$120^\circ + m\angle C = 180^\circ$
To find $m\angle C$, we subtract $120^\circ$ from both sides:
$m\angle C = 180^\circ - 120^\circ$
$m\angle C = 60^\circ$
Therefore, the measure of angle C is $60^\circ$.
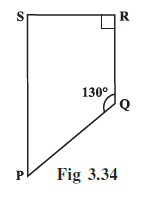
Question 12. Find the measure of ∠P and ∠S if $\overline{SP}$ || $\overline{RQ}$ in Fig 3.34.
(If you find m∠R, is there more than one method to find m∠P?)
Answer:
Given:
The figure is a quadrilateral PQRS where side $\overline{SP}$ is parallel to side $\overline{RQ}$ (SP || RQ). This means the figure is a trapezium.
We are also given the measures of two angles:
$m\angle Q = 130^\circ$
$m\angle R = 90^\circ$ (indicated by the right-angle symbol)
To Find:
The measures of $\angle P$ and $\angle S$.
Solution:
Finding the measure of $\angle P$:
Since SP || RQ, we can consider the line segment PQ as a transversal intersecting these parallel lines.
The angles $\angle P$ and $\angle Q$ are consecutive interior angles on the same side of the transversal. The sum of such angles is $180^\circ$.
$m\angle P + m\angle Q = 180^\circ$
(Sum of consecutive interior angles)
Substituting the given value of $m\angle Q = 130^\circ$:
$m\angle P + 130^\circ = 180^\circ$
$m\angle P = 180^\circ - 130^\circ$
$m\angle P = 50^\circ$
Finding the measure of $\angle S$:
Similarly, with SP || RQ, we can consider the line segment SR as another transversal.
The angles $\angle S$ and $\angle R$ are consecutive interior angles on the same side of this transversal. Their sum is also $180^\circ$.
$m\angle S + m\angle R = 180^\circ$
(Sum of consecutive interior angles)
Substituting the given value of $m\angle R = 90^\circ$:
$m\angle S + 90^\circ = 180^\circ$
$m\angle S = 180^\circ - 90^\circ$
$m\angle S = 90^\circ$
Is there more than one method to find m∠P?
Yes, there is another method to find $m\angle P$, provided we have first found $m\angle S$. This method uses the angle sum property of a quadrilateral.
Method 1: Using Consecutive Interior Angles (as shown above)
This is the most direct method. Since SP || RQ, we use the property that $m\angle P + m\angle Q = 180^\circ$ to find $m\angle P = 50^\circ$.
Method 2: Using the Angle Sum Property of a Quadrilateral
The sum of all interior angles of any quadrilateral is $360^\circ$.
$m\angle P + m\angle Q + m\angle R + m\angle S = 360^\circ$
(Angle sum property)
For this method, we first need to find $m\angle S$ (which we found to be $90^\circ$). Then we can substitute the known values into the equation:
$m\angle P + 130^\circ + 90^\circ + 90^\circ = 360^\circ$
$m\angle P + 310^\circ = 360^\circ$
$m\angle P = 360^\circ - 310^\circ$
$m\angle P = 50^\circ$
Both methods yield the same result.
Example 7 & 8 (Before Exercise 3.4)
Example 7: RICE is a rhombus (Fig 3.36). Find x, y, z. Justify your findings.
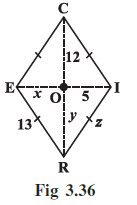
Answer:
Given:
The figure RICE is a rhombus. The diagonals intersect at point O.
The lengths of the segments are given as:
- EO = $x$
- OI = 5
- OC = 12
- OR = $y$
- ER = 13
- RI = $z$
To Find:
The values of $x$, $y$, and $z$.
Solution:
We will use the properties of a rhombus to find the values of the unknowns.
Finding the value of x:
One of the properties of a rhombus is that its diagonals bisect each other. This means they cut each other into two equal halves at their point of intersection.
For the diagonal EI, the point O is the midpoint. Therefore, the length of segment EO is equal to the length of segment OI.
EO = OI
(Diagonals of a rhombus bisect each other)
Substituting the given values:
$x = 5$
Finding the value of y:
Using the same property, the diagonal RC is also bisected at point O. This means the length of segment OR is equal to the length of segment OC.
OR = OC
(Diagonals of a rhombus bisect each other)
Substituting the given values:
$y = 12$
Finding the value of z:
A key property of a rhombus is that all four of its sides are equal in length.
RI = ER = EC = CR
(All sides of a rhombus are equal)
We are given the length of side ER as 13 and the length of side RI as $z$.
Therefore, $z = 13$.
Justification and Summary:
The values are:
- $x = 5$ because the diagonals of a rhombus bisect each other.
- $y = 12$ because the diagonals of a rhombus bisect each other.
- $z = 13$ because all sides of a rhombus are equal in length.
Alternate Method for finding z:
Another property of a rhombus is that its diagonals are perpendicular bisectors of each other. This means they intersect at a right angle ($90^\circ$).
Therefore, the triangle $\triangle ROI$ is a right-angled triangle with the right angle at O.
We can apply the Pythagorean theorem to this triangle: $OR^2 + OI^2 = RI^2$.
We have already found OR = $y = 12$ and we are given OI = 5. The hypotenuse is RI = $z$.
$12^2 + 5^2 = z^2$
$144 + 25 = z^2$
$169 = z^2$
$z = \sqrt{169}$
$z = 13$
This confirms our earlier finding.
Example 8: RENT is a rectangle (Fig 3.41). Its diagonals meet at O. Find x, if OR = 2x + 4 and OT = 3x + 1.
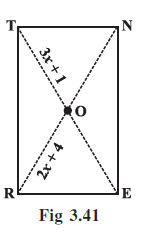
Answer:
Given:
The figure RENT is a rectangle.
The diagonals intersect at point O.
The length of segment OR is given by the expression $2x + 4$.
The length of segment OT is given by the expression $3x + 1$.
To Find:
The value of x.
Solution:
We will use the properties of the diagonals of a rectangle to find the value of x.
A fundamental property of a rectangle is that its diagonals are equal in length and they bisect each other. This means that the intersection point O is the midpoint of both diagonals, RE and TN.
Since the full diagonals are equal (RE = TN), their halves must also be equal. Therefore, all four segments from the vertices to the intersection point are equal in length.
This gives us the relationship: OR = OE = OT = ON.
Based on this property, we can set the length of segment OR equal to the length of segment OT.
OR = OT
(Segments of diagonals of a rectangle are equal)
Now, we substitute the given algebraic expressions for OR and OT into this equation:
$2x + 4 = 3x + 1$
To solve for x, we need to gather the terms involving x on one side of the equation and the constant terms on the other side.
Subtract $2x$ from both sides:
$4 = (3x - 2x) + 1$
$4 = x + 1$
Now, subtract 1 from both sides to isolate x:
$4 - 1 = x$
$3 = x$
Therefore, the value of x is 3.
Exercise 3.4
Question 1. State whether True or False.
(a) All rectangles are squares
(b) All rhombuses are parallelograms
(c) All squares are rhombuses and also rectangles
(d) All squares are not parallelograms.
(e) All kites are rhombuses.
(f) All rhombuses are kites.
(g) All parallelograms are trapeziums.
(h) All squares are trapeziums.
Answer:
(a) All rectangles are squares.
False. A square is a rectangle with all sides equal. Rectangles do not necessarily have all sides equal.
(b) All rhombuses are parallelograms.
True. A rhombus is a quadrilateral with all four sides equal. This implies that opposite sides are parallel, which is the definition of a parallelogram.
(c) All squares are rhombuses and also rectangles.
True. A square has four equal sides, which satisfies the definition of a rhombus. A square has four right angles, which satisfies the definition of a rectangle.
(d) All squares are not parallelograms.
False. A square has opposite sides parallel and equal, which means it is a parallelogram.
(e) All kites are rhombuses.
False. A kite has two pairs of equal adjacent sides. A rhombus has all four sides equal. A kite does not necessarily have all four sides equal.
(f) All rhombuses are kites.
True. A rhombus has all four sides equal. This means it has two pairs of equal adjacent sides (e.g., side1=side2 and side3=side4, and since all are equal, side1=side2=side3=side4), which satisfies the definition of a kite.
(g) All parallelograms are trapeziums.
True. A parallelogram has two pairs of parallel opposite sides. A trapezium is a quadrilateral with at least one pair of parallel sides. Since a parallelogram has two pairs, it satisfies the condition of having at least one pair.
(h) All squares are trapeziums.
True. A square is a parallelogram (from part c and d). All parallelograms are trapeziums (from part g). Therefore, all squares are trapeziums.
Question 2. Identify all the quadrilaterals that have.
(a) four sides of equal length
(b) four right angles
Answer:
(a) Quadrilaterals that have four sides of equal length:
The quadrilaterals that have four sides of equal length are:
1. Rhombus: By definition, a rhombus is a quadrilateral with all four sides of equal length.
2. Square: A square is a special type of rhombus where all angles are right angles. Since a square is a rhombus, it also has four sides of equal length.
(b) Quadrilaterals that have four right angles:
The quadrilaterals that have four right angles are:
1. Rectangle: By definition, a rectangle is a quadrilateral with four right angles.
2. Square: A square is a special type of rectangle where all four sides are equal in length. Since a square is a rectangle, it also has four right angles.
Question 3. Explain how a square is.
(i) a quadrilateral
(ii) a parallelogram
(iii) a rhombus
(iv) a rectangle
Answer:
(i) How a square is a quadrilateral:
A quadrilateral is a polygon with four sides.
A square has exactly four sides and four vertices. Therefore, by definition, a square is a quadrilateral.
(ii) How a square is a parallelogram:
A parallelogram is a quadrilateral with opposite sides parallel.
A square is a quadrilateral where all four angles are $90^\circ$. This property implies that consecutive interior angles are supplementary ($90^\circ + 90^\circ = 180^\circ$), which in turn implies that opposite sides are parallel.
Also, a square has opposite sides of equal length, which is another property of a parallelogram. Since a square has both pairs of opposite sides parallel (and equal), it is a parallelogram.
(iii) How a square is a rhombus:
A rhombus is a quadrilateral with all four sides of equal length.
A square is defined as a quadrilateral with all four sides equal in length and all four angles equal to $90^\circ$. Since a square meets the condition of having all four sides of equal length, it is a rhombus.
(iv) How a square is a rectangle:
A rectangle is a quadrilateral with four right angles.
A square is defined as a quadrilateral with all four sides equal in length and all four angles equal to $90^\circ$. Since a square meets the condition of having four right angles, it is a rectangle.
Question 4. Name the quadrilaterals whose diagonals.
(i) bisect each other
(ii) are perpendicular bisectors of each other
(iii) are equal
Answer:
(i) Quadrilaterals whose diagonals bisect each other:
The property that diagonals bisect each other is a characteristic of all parallelograms.
Quadrilaterals that are parallelograms include:
• Parallelogram (general)
• Rectangle (a type of parallelogram)
• Rhombus (a type of parallelogram)
• Square (a type of parallelogram, rhombus, and rectangle)
So, the quadrilaterals whose diagonals bisect each other are Parallelograms, Rectangles, Rhombuses, and Squares.
(ii) Quadrilaterals whose diagonals are perpendicular bisectors of each other:
This means the diagonals bisect each other and are also perpendicular.
Quadrilaterals whose diagonals are perpendicular bisectors of each other are:
• Rhombus: The diagonals of a rhombus bisect each other and are perpendicular.
• Square: A square is a type of rhombus, so its diagonals also have this property.
So, the quadrilaterals whose diagonals are perpendicular bisectors of each other are Rhombuses and Squares.
(iii) Quadrilaterals whose diagonals are equal:
Quadrilaterals whose diagonals are equal in length are:
• Rectangle: The diagonals of a rectangle are equal in length and bisect each other.
• Square: A square is a type of rectangle, so its diagonals are also equal in length.
• Isosceles Trapezium: An isosceles trapezium is a trapezium where the non-parallel sides are equal. The diagonals of an isosceles trapezium are equal in length.
So, the quadrilaterals whose diagonals are equal are Rectangles, Squares, and Isosceles Trapeziums.
Question 5. Explain why a rectangle is a convex quadrilateral.
Answer:
Explanation:
A convex quadrilateral is defined as a quadrilateral in which all interior angles are less than $180^\circ$.
In a rectangle, all four interior angles are right angles, meaning each angle measures exactly $90^\circ$.
Measure of each interior angle = $90^\circ$
Since $90^\circ < 180^\circ$, all interior angles of a rectangle are less than $180^\circ$.
Alternatively, another property of a convex quadrilateral is that the line segment connecting any two points within or on its boundary lies entirely within or on the boundary of the quadrilateral. In a rectangle, drawing any line segment between two points inside the rectangle will always keep the segment inside the rectangle.
Therefore, because all its interior angles are less than $180^\circ$ (or because any segment between two interior points remains interior), a rectangle fits the definition of a convex quadrilateral.
Question 6. ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).

Answer:
Given:
ABC is a right-angled triangle, with the right angle at B ($m\angle B = 90^\circ$).
O is the midpoint of the hypotenuse AC.
To Explain:
Why point O is equidistant from the vertices A, B, and C (i.e., why OA = OB = OC).
Explanation:
We can use the properties of a rectangle to explain this relationship. The dotted lines in the figure help us visualize this.
Step 1: Constructing a rectangle
Let's use the provided hint and draw additional lines. We draw a line from A parallel to BC, and a line from C parallel to AB. Let these lines meet at a point D. This completes the quadrilateral ABCD.
AB || DC and BC || AD
(By construction)
Since both pairs of opposite sides are parallel, the quadrilateral ABCD is a parallelogram.
We are given that $\angle B = 90^\circ$. A parallelogram with one right angle is a rectangle.
Therefore, ABCD is a rectangle.
Step 2: Using the properties of a rectangle's diagonals
In a rectangle, the diagonals have two important properties:
- They are equal in length.
- They bisect each other (i.e., they cut each other into two equal halves at their intersection point).
In our rectangle ABCD, the diagonals are AC and BD. They intersect at the point O.
According to the properties:
AC = BD
(Diagonals are equal in length)
Also, since the diagonals bisect each other at O, O is the midpoint of both AC and BD.
This means that all four segments from the vertices to the center point O are equal.
OA = OC = $\frac{1}{2}$ AC
OB = OD = $\frac{1}{2}$ BD
Since AC = BD, it follows that $\frac{1}{2}$ AC = $\frac{1}{2}$ BD.
Therefore, we can conclude that:
OA = OB = OC = OD
Step 3: Conclusion
From the relationship derived above, we can clearly see that OA = OB = OC.
This shows that the distance from point O to vertex A, vertex B, and vertex C is the same. Hence, O is equidistant from A, B, and C.

